2024年河南成人高考高起点理科数学预测真题及答案（一）

　　本试卷分选择题和非选择题两部分.满分l50分，考试时间l20分钟.

　　选择题

　　一、选择题：本大题共l7小题，每小题5分，共85分.在每小题给出的四个选项中，只有一项是符合题目要求的.

　　(1)已知集合A={1，2，3，4，6，12}，C={1，2，3，6，9，18}，则A∩C=

　　A.{1，2，3，4，6，9，12，18}

　　B.{1,2，3，6}

　　C.{1，3，6}

　　D.{1，2，6}

　　(2)(1+i)4的值是(成人高考更多完整资料免费提供加微信/QQ：29838818)

　　A.2 B.2i C.4 D.-4

(3)

　　A.-2 B.-1 C.0 D.1

　　(4)若向量a=(1，2)，b=(-3，4)，则(a·b)(a+b)等于

　　A.20 B.(-10，30) C.54 D.(-8，24)

　　(5)棱长为a的正方体，其外接球的表面积为

　　A.πa2B.4πa2C.3πa2D.12πa2

　　(6)三角形全等是三角形面积相等的

　　A.充分但不必要条件 B.必要但不充分条件

　　C.充要条件 D.既不充分也不必要条件

　　(7)已知y=f(x)(x∈R)是以4为周期的奇函数，且f(l)=1,f(3)=a，则有

　　A.a=1 B.a=2 C.a=-1 D.a=-2

　　(8)等差数列{an}的公差d<0，且n2·n4=12，a2+a4=8，则数列{an}的通项公式是

　　A.an=2n-2(n∈N*)B.an=2n+4(n∈N*)

　　C.an=-2n+12(n∈N*) D.an=-2n+10(n∈N*)

　　(9)方程2x2-5x+2=0的两根可分别作为

　　A.一个椭圆和一个双曲线的离心率 B.两个抛物线的离心率

　　C.一个椭圆和一个抛物线的离心率 D.两个椭圆的离心率

　　(10)甲、乙两人独立地解同一个问题，甲解决这个问题的概率是P1，乙解决这个问题的概率是P2，那么其中至少有1人解决这个问题的概率是

　　A.P1+P2B.P1P2C.1-P1P2D.1-(1-P1)(1一P2)

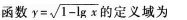
(11)

　　A.{x|x>0} B.{x|0

　　(12)5个人排成一排，甲、乙相邻的不同排法有

　　A.60种 B.48种 C.36种 D.24种

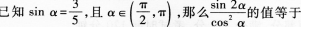
(13)

　　(14)抛物线y=ax2的准线方程是y=2，则a的值为

　　(15)一名同学投篮的命中率为2/3，他连续投篮3次，其中恰有2次命中的概率p为

　　(16)直线Y=ax+2与直线Y=3x-b关于直线y=x对称，则

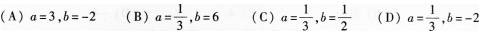
　　(17)函数Y=1+3x-x3有

　　A.极小值-1，极大值1 B.极小值-2，极大值3

　　C.极小值-2，极大值2 D.极小值-1，极大值3

非选择题

　　二、填空题：本大题共4小题，每小题4分，共l6分.把答案填在题中横线上.

(18)(成人高考更多完整资料免费提供加微信/QQ：29838818)

　　(19)设(x+2)4=a0x4+a1x3+a2x2+a3x+a4,则a4=____.

　　(20)函数y=4sin xcosx的最小正周期及最大值分别是____.

　　(21)曲线y=2x2-1在点(1，1)处的切线方程是___.

　　三、解答题：本大题共4小题，共49分.解答应写出推理、演算步骤.

　　(22)(本小题满分l2分)

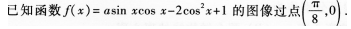
　　(I)求实数a的值;

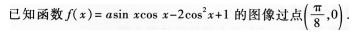
(II)

　　(23)(本小题满分12分)

　　已知等差数列{an}中，a1=9，a3+a8=0.

　　(I)求数列{an}的通项公式;

　　(Ⅱ)当n为何值时，数列{an}的前n项和Sn取得最大值，并求该最大值.

　　(24)(本小题满分12分)

　　已知抛物线C：x2=2py(p>O)的焦点F在直线l:x-y+1=0上.

　　(I)求抛物线C的方程;

　　(Ⅱ)设直线f与抛物线C相交于P，Q两点，求线段PQ中点M的坐标.

　　(25)(本小题满分l3分)

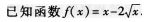
　　(I)求函数y=f(x)的单调区间，并指出它在各单调区间上是增函数还是减函数;

　　(Ⅱ)求函数y=f(x)在区间[0，4]上的最大值和最小值.

　　答案解析

　　一、选择题

　　(1)【参考答案】 (B)

　　集合A∩C是由同时属于集合A和集合C的元素组成的集合，易得答案为A∩C={1，2，3,6}.

　　【解题指要】本题考查集合的运算.注意A∪C的结果是(A)，二者是不同的.

　　(2)【参考答案】 (D)

　　(1+i)4=[(1+i)2]2=(2i)2=-4.

　　【解题指要】本题考杏复数运算.在复数运算中，要记住：

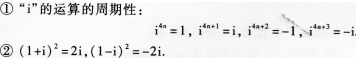
　　(3)【参考答案】 (A)

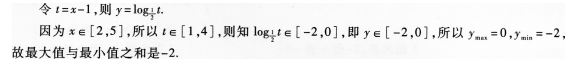
　　【解题指要】本题考查函数值域的求法，一般采用直接法求解.

　　(4)【参考答案】 (B)

　　(a·b)(a+b)=[(1，2)·(-3，4)][(1，2)+(-3，4)] =(-3+8)(-2，6)=5(-2，6)=(-l0，30).

　　【解题指要】本题考查向量的运算.向量数量积的结果是实数，向量和数的乘积的结果是

　　向量.

　　(5)【参考答案】 (C)

　　【解题指要】本题考查正方体和球的相关知识.

　　(6)【参考答案】 (A)

　　若两个三角形全等，则它们的面积相等;然而，面积相等的三角形却不一定是全等三角形，因此答案为充分但不必要条件，选(A).

　　【解题指要】本题考查充分必要条件的相关知识.

　　(7)【参考答案】 (C)

　　因为f(x)是以4为周期的奇函数，所以

　　f(3)=f(3-4)=f(-l)=-f(1)，

　　即a=-f(1).

　　又f(1)=1，所以a=-1.

　　【解题指要】本题考查函数的奇偶性和周期性.

　　(8)【参考答案】 (D)

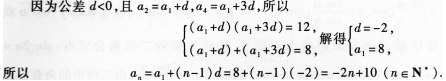
　　【解题指要】本题考查等差数列的通项公式.

　　(9)【参考答案】(A)

　　【解题指要】本题考查离心率的相关知识.椭圆离心率的取值范围是(0，1)，双曲线离心率的取值范围是(1，+∞)，抛物线的离心率为1.

　　(10)【参考答案】 (D)

　　【解题指要】本题考查独立事件同时发生的概率.甲不能解决问题的概率为1-P1，乙不能解决问题的概率为1-p2，因此，两人都不能独立解决问题的概率为(1-p1)(1-p2)，从而其中至少有1人解决这个问题的概率为1-(1-p1)(1-p2).

　　(11)【参考答案】 (B)

　　二次根式要有意义，应有1-lg x≥0，即lg x≤1=lg 10，所以0

　　【解题指要】本题考查二次根式的概念和对数函数的单调性，求解时要注意对数函数的定

　　义域.

　　(12)【参考答案】 (B)

　　【解题指要】本题考查排列组合的相关知识.对于相邻问题，采用捆绑法比较方便求解.

　　(13)【参考答案】 (B)

　　(14)【参考答案】 (B)

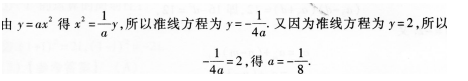
　　【解题指要】本题考查抛物线的标准方程及其相关几何性质.抛物线的标准方程形式：二

　　几何性质.

　　(15)【参考答案】 (D)

　　【解题指要】本题考查n次独立重复事件概率的计算方法.

　　(16)【参考答案】 (B)

　　【解题指要】本题考查反函数的求法.求反函数要先“倒”：即把x用y表示;然后“换”：即

　　x换成y，y换成x;最后“注”：注明反函数的定义域(即原函数的值域).

　　(17)【参考答案】 (D)

　　由于y’=3-3x2，x=±1时,y’=0，且x<-1时，y’<0;-1

　　【解题指要】本题考查导数的应用.注意导数值为0的点，需它的“左邻”和。“右邻”的导数异号.才能判断其为极值点，若两侧导数同号则不行.例如y=x3，y'=3x2，当x=0时.虽然y'=0.但是x>0时y’>0，x

　　二、填空题

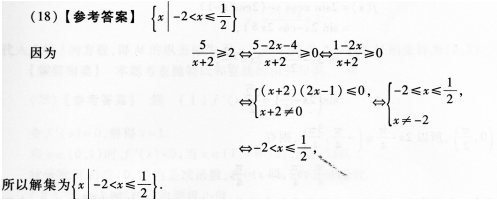
　　【解题指要】本题考查分式不等式的解法，其基本步骤如下：①移项;②通分;③转化为

　　整式不等式.

　　求解本题时要注意分母不为0这一条件.

　　(19)【参考答案】 l6

　　根据二项式定理，可知a4=24=16.【解题指要】 本题考查二项式定理.

　　(20)【参考答案】 π，2

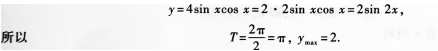
　　【解题指要】本题考查二倍角的正弦公式、三角函数的周期与最值等知识.

　　(21)【参考答案】4x-Y-3=0

　　【解题指要】本题考查二倍角的正弦公式和余弦公式，考查两角差的三角函数公式.本题

　　(23)【参考答案】

　　解(I)设等差数列{an}的公差为d，由已知a3+a8=0，得2a1+9d=0.又已知a1=9，所以d=-2.

　　数列{an}的通项公式为

　　an=9-2(n一l)，即an=11-2n.

　　(Ⅱ)数列{an}的前n项和

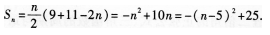
　　当n=5时，Sn取得最大值25.

　　也可采用下面的方法：因为该等差数列递减，要求其前n项和的最大值，只需关注该数列的

　　正项即可.令an=11-2n>0，得n<11/2，即取n为5.

　　易知数列的前5项依次为：9，7，5，3，1，故前n项和的最大值为

　　S5=9+7+5+3+1=25.

　　此法也是常见思路之一.

　　【解题指要】本题考查等差数列的通项公式和前n项和公式.

　　(24)【参考答案】

　　解(I)由抛物线方程x2=2py(p>0)为标准方程，知其焦点在y轴正半轴上.在直线x-y+1=0中，令x=0，得焦点坐标为F(0，1)，所以p/2=1，即P=2，故抛物线C的方程是x2=4y.

　　(Ⅱ)设P，Q的坐标分别为(x1，y1)，(x2，y2).

　　代入直线l的方程，得M的纵坐标为yM=3，所以线段PQ中点M的坐标为(2，3).

　　【解题指要】本题考查抛物线和直线的相关知识.

　　【解题指要】本题考查导数的应用：用导数判断函数的单调区间和求函数的最大值、最小值.